Force/Moment Convention
Positive conventions for internal forces and bending moments
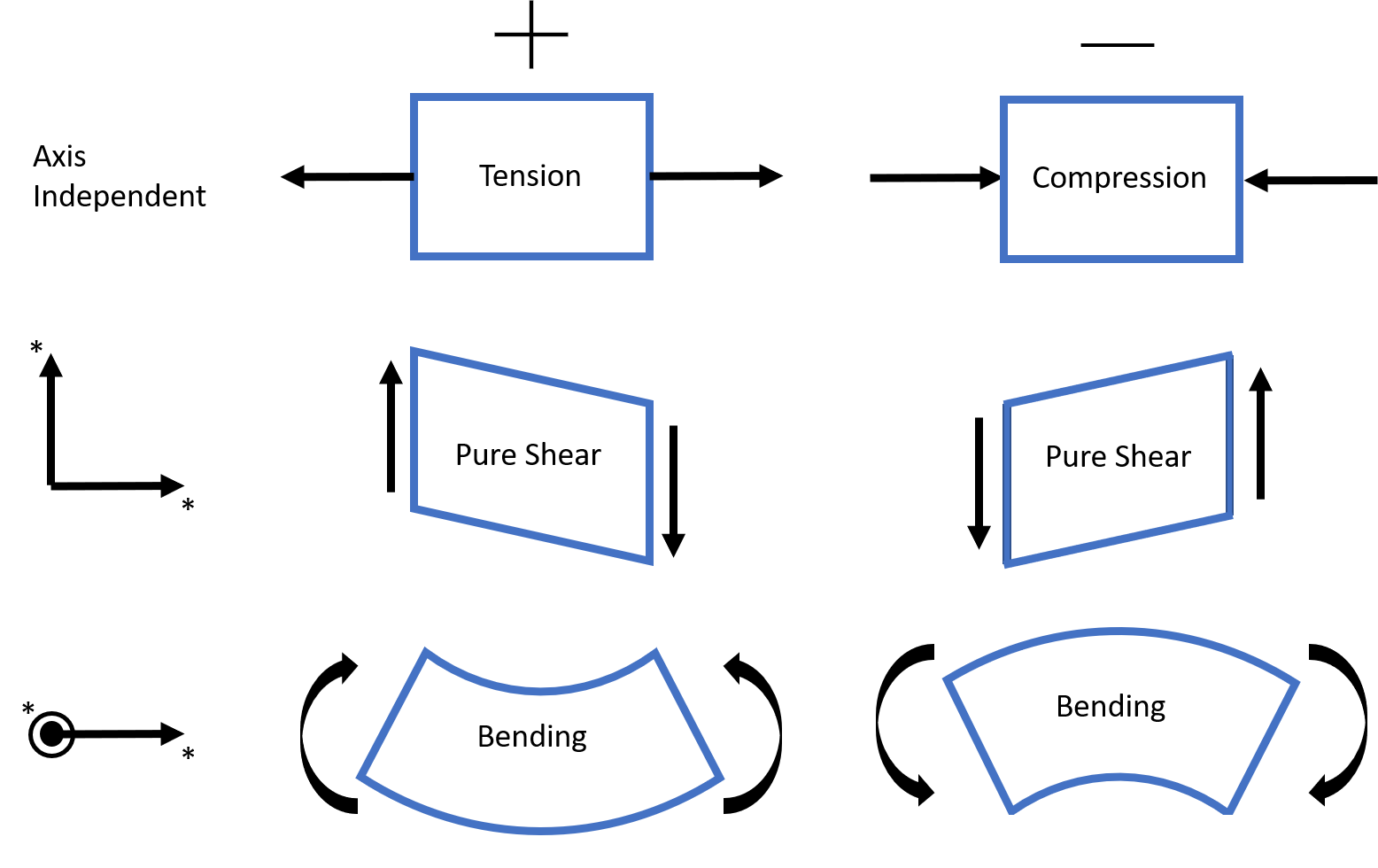
Expanded to 2D cuts
Expanded to 3D cuts
Selection of coordinate axes "x-y-z" is completely arbitrary. This sign convention is true for any right-handed coordinate system "1-2-3"
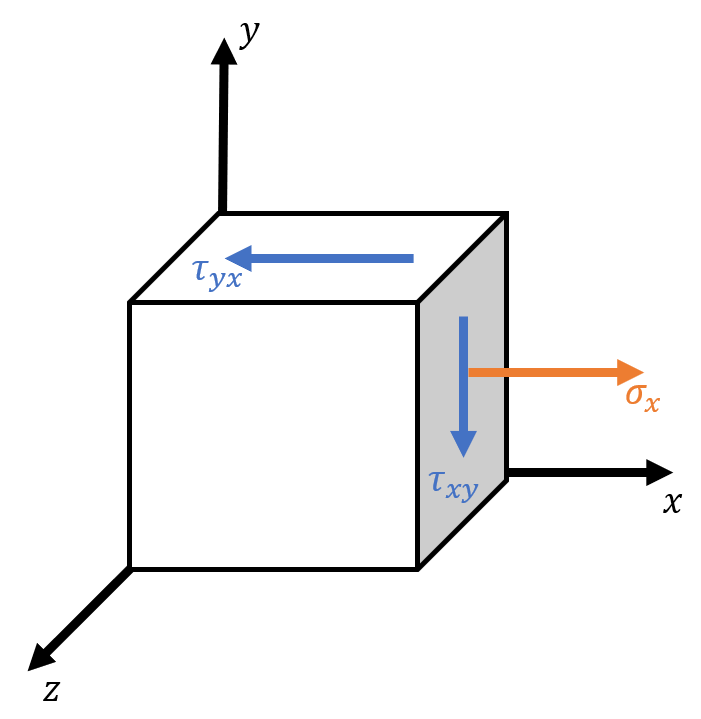
Stress Convention
Positive Sign Convention for Stress
A 3D-stress element is a representation of the state of stress composed of six stress components: $\sigma_x, \sigma_y, \sigma_z, \tau_{xy}, \tau_{yz}, \rm\ and \ \tau_{zx}$. The positive face of each plane is shown in this diagram.
Normal Stress: As with internal forces, a positive normal stress, $\sigma$ points away from the stress element. Tension is positive (pulling apart) and compression is negative (pushing together).
Shear Stress: For shear stresses, there are two subscripts. The first subscript denotes the face on which the stress acts and the second is the direction on that face. For example, a positive $\tau_{xy}$ is represented on the $x$-plane, pointing in the direction of the $y$-axis. A shear stress is positive if it acts on a positive face in a positive direction or if it acts on a negative face in a negative direction.
Example: Finding the Infinitesimal Stress Element
In this example, we will use the positive convention for internal loads and moments at a cross-section and use them to determine the existing stresses at each point, $H$ and $K$.
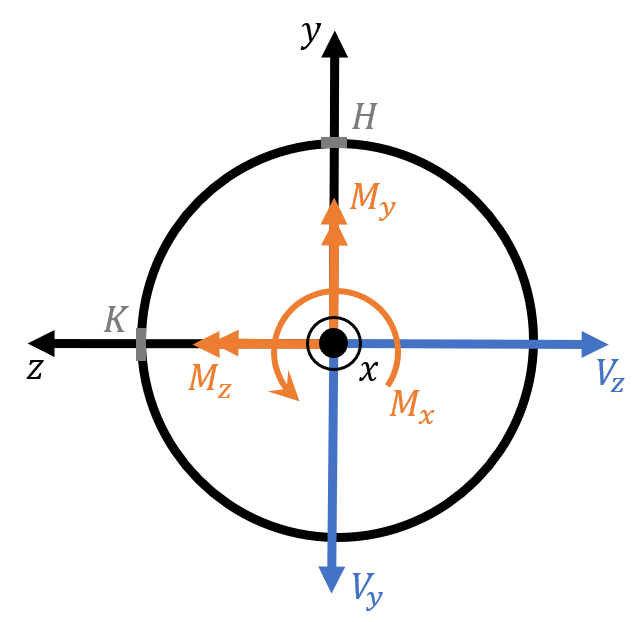
We will also assume we have all necessary values for calculating the stresses: $d$, $A$, $Q$, $I$.
Point H
\[\tau_{xy}^{H} = \frac{V_y Q}{I d}=0 \ (d=0)\]
\[\tau_{xz}^{H} = \frac{M_x\frac{d}{2}}{J} - \frac{V_z Q}{I d} (Q = \rm\ first \ moment)\]
\[\sigma_{x}^{H} = \frac{F_x}{A} - \frac{M_z \frac{d}{2}}{I}\]
Understanding Shear Stress: $V_z$ is considered a positive internal shear force. However, in the superposition equation for $\tau_{xz}$, the stress due to $V_z$ is negative. A positive shear stress $\tau_{xz}$ points in the positive $z$-direction on the positive $x$-face, therefore, the shear stress due to a positive internal shear force $V_z$ is negative.
The same logic applies to the sign of the shear stress due to the torsion $T=M_x$. A positive torque would induce a shear pointing in the positive $z$-direction at point $H$.
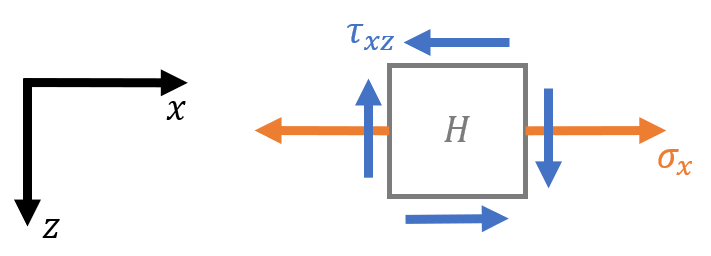
Assuming the normal stress $\sigma_x$ and the shear stress $\tau_{xz}$ are positive, this is the 3D stress element:

Note that all relevant (non zero) components lie in the x-z plane. Therefore, when representing the stress element for point 𝐻, we use the x-z plane.
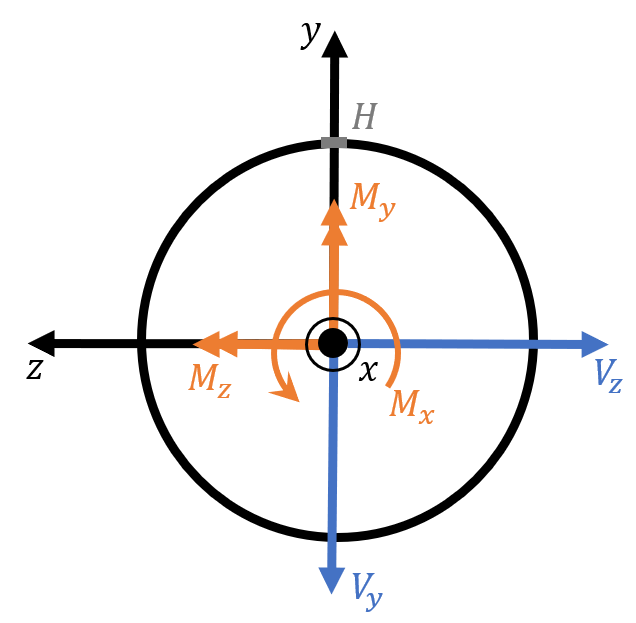
Point K
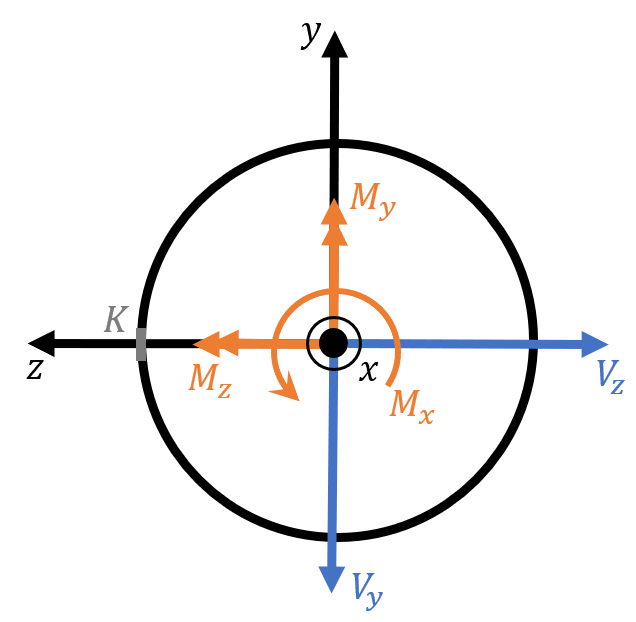
\[\tau_{zy}^{K} = \frac{V_z Q}{I d}=0 \ (d=0) \]
\[\tau_{xy}^{K} = - \frac{M_x\frac{d}{2}}{J} - \frac{V_y Q}{I d} (Q = \rm\ first \ moment)\]
\[\sigma_{x}^{K} = \frac{F_x}{A} + \frac{M_y \frac{d}{2}}{I}\]
Assuming the normal stress $\sigma_x$ is positive and the shear stress $\tau_{xy}$ is negative, this is the 3D stress element:
Note that all relevant (non zero) components lie in the x-y plane. Therefore, when representing the stress element for point 𝐻, we use the x-y plane.
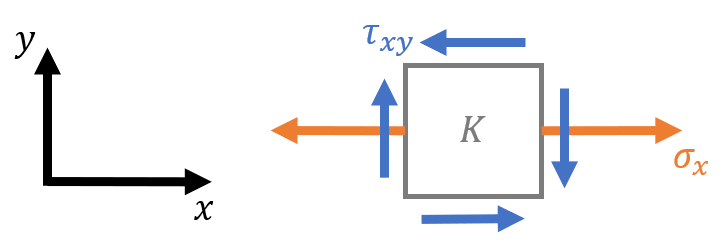
There are different conventions for shear forces and shear stresses. See the example for more detail.