Deflection of Beams
Goal: Determine the deflection and slope at specified points of beams and shafts
Solve statically indeterminate beams: where the number of reactions at the supports exceeds the number of equilibrium equations available.
Maximum deflection of the beam: Design specifications of a beam will generally include a maximum allowable value for its deflection
Elastic Curve of Beam:

Assume bending only: we will neglect effects of transverse shear
Moment-curvature equation: $M(x) = \frac{E(x)I(x)}{\rho(x)}$ \[\kappa = \frac{1}{\rho} = \frac{M(x)}{EI}\]

Governing equation of the elastic curve \[\frac{d^2y}{dx^2} = \frac{M(x)}{EI}\]
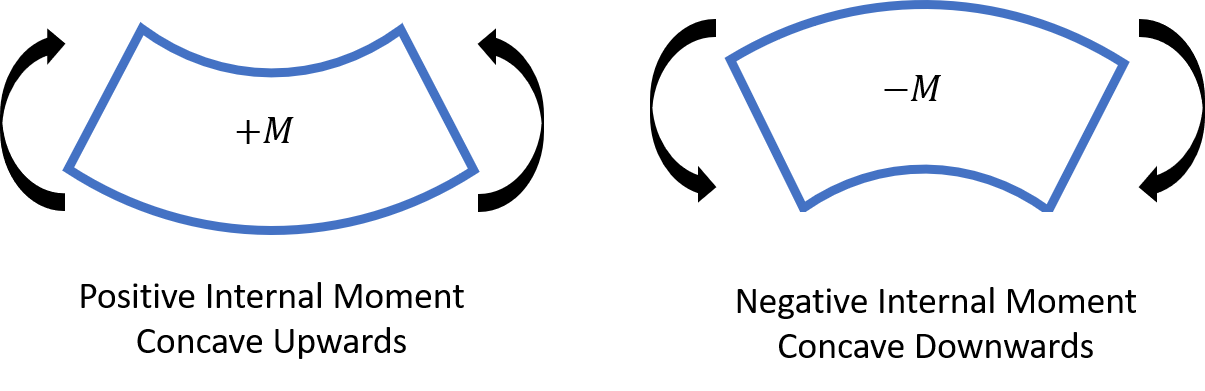
Sign Conventions:
Boundary Conditions:

\[\begin{align} \theta &\ne 0 \\ y &= 0 \\ M &= 0 \\ V &= R \end{align}\]
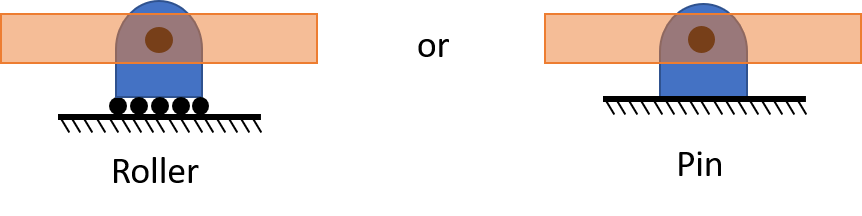
\[\begin{align} \theta &\ne 0 \\ y &= 0 \\ M &\ne 0 \\ \Delta V &= R \end{align}\]

\[\begin{matrix} \begin{align} \rm\ Fixed &\rm\ End: & \rm\ Free &\rm\ End: \\ \theta &= 0 & \theta &\ne 0 \\ y &= 0 & y &\ne 0 \\ M &\ne 0 & M &= 0 \\ V &\ne 0 & V &= 0 \end{align} \end{matrix}\]

\[\begin{align} \theta &\ne 0 \\ y &\ne 0 \\ M &= 0 \\ V &\ne 0 \end{align}\]
Integration Methods:
Elastic curve equation for constant E and I: $EIy'' = M(x)$
Differentiating both sides gives: $EIy''' = \frac{dM(x)}{dx} = V(x)$
Differentiating again: $EIy'''' = \frac{dV(x)}{dx} = w(x)$
In summary, we have: \[\begin{align} V(x) &= \int w(x) dx \\ M(x) &= \int V(x)dx \\ \frac{dy}{dx} &= \int \frac{1}{EI}M(x)dx \\ y(x) &= \int y'(x) dx \end{align}\]
Where:
$y(x):$ deflection
$y'(x):$ slope
$EIy''(x):$ bending moment
$EIy'''(x):$ shear force
$EIy''''(x):$ distributed load
Example 1: Overhanging beam

Example 2: Cantilever beam

Superposition Principle:
